3D Poisson Equation

Background

Let $\Omega \!\subset\!\mathbb{R}^3$ be a bounded, simply or multiply connected domain in 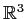with a Lipschitz boundary 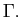The Poisson equation for a scalar function in 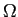is given by

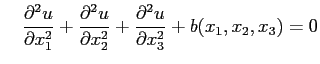
$\displaystyle \Delta u(\boldsymbol{x})+b(\boldsymbol{x})=0$ or $\displaystyle \quad\nabla^2u(\boldsymbol{x})+b(\boldsymbol{x})=0$ or $\displaystyle \quad \frac{\partial^2u}{\partial x_1^2} + \frac{\partial^2u}{\partial x_2^2}+ \frac{\partial^2u}{\partial x_3^2} + b(x_1,x_2,x_3)= 0$

where represents a source function prescribed on $\overline{\Omega}\!=\!\Omega\cup\Gamma$ .

A solution of the Poisson equation admits an integral representation, known as the Green's representation formula, expressed as

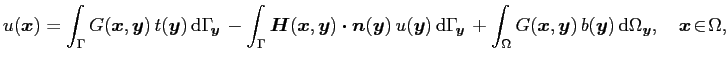
$\displaystyle u(\boldsymbol{x}) = \int_{\Gamma }G(\boldsymbol{x},\boldsymbol{y}... ...symbol{y}) {\rm d}\Omega _{\boldsymbol{y}}, \quad\boldsymbol{x}\!\in\!\Omega ,$

where $\boldsymbol{n}$ is the unit normal to $\Gamma$ directed towards the exterior of $\Omega ;$ $t=\partial u/\partial n$ is the flux associated with the function and the kernels and $\boldsymbol{H}$ are given respectively by

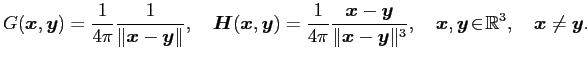
$\displaystyle G(\boldsymbol{x},\boldsymbol{y})=\frac1{4\pi}\frac1{\Vert\boldsym... ...mbol{x},\boldsymbol{y}\!\in\!\mathbb{R}^3,\quad\boldsymbol{x}\ne\boldsymbol{y}.$

Here $\Vert\boldsymbol{x}\Vert$ is the usual Euclidean norm in $\mathbb{R}^3$ defined as $\Vert\boldsymbol{x}\Vert=\sqrt{x_1^2+x_2^2+x_3^2}$ . In addition, it was established in [1] that the Newton potential admits a boundary representation as

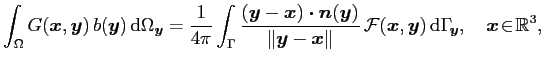
$\displaystyle \int_{\Omega }G(\boldsymbol{x},\boldsymbol{y}) b(\boldsymbol{y})... ...{y}) {\rm d}\Gamma _{\!\boldsymbol{y}},\quad\boldsymbol{x}\!\in\!\mathbb{R}^3,$

where

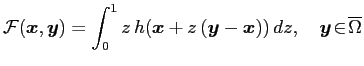
$\displaystyle \mathcal{F}(\boldsymbol{x},\boldsymbol{y})=\int_{0}^{1}z h(\bold... ...oldsymbol{y}-\boldsymbol{x})) dz,\quad \boldsymbol{y}\!\in\!\overline{\Omega }$

with denoting an extension of the source function into any ball centered at $\boldsymbol{x}$ and containing $\overline{\Omega }$ . In particular, a continuation of the source function can be specified as

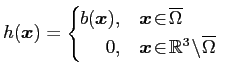
$\displaystyle h(\boldsymbol{x}) = \left\{ \begin{array}{rl} \!\!\!b(\boldsymbol... ...ymbol{x}\!\in\! \mathbb{R}^3\!\setminus\!\overline{\Omega } \end{array} \right.$

This representation of the Newton potential in term of surface integral allows a numerical solution of the Poisson equation that does not require a volume-fitted mesh.

Solution via a boundary element method

To approximately solve the Poisson equation via a Boundary Element Method (BEM), the surface $\Gamma$ is usually discretized into flat triangles $\Gamma _j$ using a mesh generation software (e.g. CUBIT).