Collocation BEM for 3D Lame Equation

Download CBEM_LAM, a package for solving the 3D Lamé equation based on a piecewise constant Collocation Boundary Element Method, and employing a boundary-only discretization technique.

 

Piecewise constant collocation method

The displacement $ \boldsymbol{u}$ and traction $ \boldsymbol{t}$are assumed to be constant over each boundary element. It can be shown (see e.g. [2]) that the elastic potentials

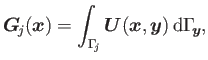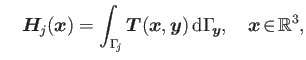
$\displaystyle \boldsymbol{G}_{\!j}(\boldsymbol{x})=\int_{\Gamma _{\!j}}\boldsymbol{U}(\boldsymbol{x},\boldsymbol{y}) {\rm d}\Gamma _{\!\boldsymbol{y}},$   and$\displaystyle \quad \boldsymbol{H}_{\!j}(\boldsymbol{x})=\int_{\Gamma _{\!j}}\b... ...{y}) {\rm d}\Gamma _{\!\boldsymbol{y}},\quad\boldsymbol{x}\!\in\!\mathbb{R}^3,$   

due to a uniform distribution over a flat triangle $ \Gamma_{\!j},$ can be employed to successfully compute $ \boldsymbol{u}$ and $ \boldsymbol{t}$ on $ \Gamma=\bigcup\overline{\Gamma_{\!j}}$ . In addition, these potentials can be utilized to effectively calculate the displacement $ \boldsymbol{u}$ at interior points $ \boldsymbol{x}\!\in\!\Omega.$ The analytic expressions for $\boldsymbol{G}_{\!j}(\boldsymbol{x})$ and $\boldsymbol{H}_{\!j}(\boldsymbol{x})$ over a flat triangle are given in [1]. Moreover, due to its boundary representation, the elastic Newton potential can also be effectively evaluated without the need of a volume-fitted mesh [2]. A brief description of the boundary-only discretization of the elastic Newton potential can be found in the user guide cbem_lamGuide.pdf provided in the package CBEM_LAM.

 

References

[1] S. Nintcheu Fata.
     Explicit expressions for three-dimensional boundary integrals in linear elasticity.
     J. Comput. Appl. Math., 235(15):4480-4495, 2011.
[2] S. Nintcheu Fata.
     Boundary integral approximation of volume potentials in three-dimensional linear elasticity.
     J. Comput. Appl. Math., 242(1):275-284, 2013.