Galerkin BEM for 3D Laplace Equation

Download GBEM_LAP, a package for solving the 3D Laplace equation based on a piecewise linear Galerkin Boundary Element Method.

 

Piecewise linear Galerkin method

The potential $u$ and flux $t$ are assumed to be linear over each boundary element. It can be shown (see [2,3,4]) that the Galerkin surface integrals

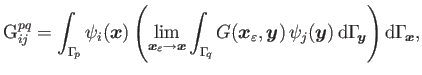$\displaystyle \mathrm{G}_{ij}^{pq}=\int_{\Gamma _{\!p}}\psi_i(\boldsymbol{x})\l... ...y}) {\rm d}\Gamma _{\!\boldsymbol{y}}\right){\rm d}\Gamma _{\!\boldsymbol{x}},$   and$\displaystyle \quad \mathrm{H}_{ij}^{pq}=\int_{\Gamma _{\!p}}\psi_i(\boldsymbol... ...y}) {\rm d}\Gamma _{\!\boldsymbol{y}}\right) {\rm d}\Gamma _{\!\boldsymbol{x}}$   

can be employed to successfully compute $u$ and $t$ on the boundary$\Gamma =\bigcup \overline{\Gamma _{\!q}},$ where $\boldsymbol{x}_{\varepsilon}$ is an exterior point to $\overline{\Omega }\!=\!\Omega \cup\Gamma ,$ $\Gamma _{\!p}\!\in\!\mathrm{supp}(\psi_i),$ $\Gamma _{\!q}\!\in\!\mathrm{supp}(\psi_j),$ and $\mathrm{supp}(\psi_j)$ stands for the support of the function $\psi_j.$ Moreover, $\psi_i$ is a linear test function defined over the flat triangle $\Gamma _{\!p}$ and $\psi_j$ is a linear shape function defined over the flat triangle $\Gamma _{\!q}.$ In addition, the following potentials

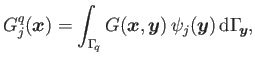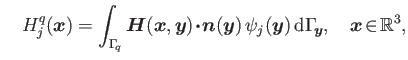
$\displaystyle G_j^{q}(\boldsymbol{x})=\int_{\Gamma _{\!q}}G(\boldsymbol{x},\boldsymbol{y}) \psi_j(\boldsymbol{y}) {\rm d}\Gamma _{\!\boldsymbol{y}},$   and$\displaystyle \quad H_j^{q}(\boldsymbol{x})=\int_{\Gamma _{\!q}}\boldsymbol{H}(... ...{y}) {\rm d}\Gamma _{\!\boldsymbol{y}},\quad\boldsymbol{x}\!\in\!\mathbb{R}^3,$   

are utilized to effectively calculate $u$ at interior points $\boldsymbol{x}\!\in\!\Omega .$ The analytic expressions for $G_j^{q}(\boldsymbol{x})$ and $H_j^{q}(\boldsymbol{x})$ over a flat triangle are given in [1].

 

References

[1] S. Nintcheu Fata.
     Explicit expressions for 3D boundary integrals in potential theory.
     Int. J. Num. Meth. Eng., 78(1):32-47, 2009.
[2] S. Nintcheu Fata and L. J. Gray.
     Semi-analytic integration of hypersingular Galerkin BIEs for three-dimensional potential problems.
     J. Comput. Appl. Math., 231(2):561-576, 2009.
[3] S. Nintcheu Fata and L. J. Gray.
     On the implementation of 3D Galerkin boundary integral equations.
     Eng. Anal. Boundary Elem., 34(1):60-65, 2010.
[4] S. Nintcheu Fata.
     Semi-analytic treatment of nearly-singular Galerkin surface integrals.
     Appl. Numer. Math., 60(10):974-993, 2010.